Hi,
I would greatly appreciate advice on interpreting a 3-way interaction between two dummy variables (treatment indicator and post-treatment-period indicator) and 1 continuous variable. Specifically, I am estimating a DiD model to evaluate the impact of a minimum wage increase. I have two periods: one pre-MW-reform-period and one post-MW-reform-period. The minimum wage is nominal and uniform across the entire country. However, inflation rates vary across states. I anticipate that the effect of the MW will be greatest, where the minimum wage has increase the most in real terms. Thus, I have made a variable, shockMW, which is captures the change in the minimum wage measured in 2018 prices, ln(real MW post/real MW pre). I have subtracted the mean value of the shock variable, so that it is evaluated at the mean.
To evaluate whether the impact of the MW increase is largest in these areas, I have estimated the following model:
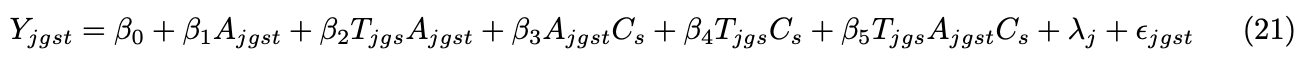
Using the following code:
reghdfe lnwage treat##year##c.shockMW, absorb(FirmID) vce(cluster FirmID)
Treat is an indicator taking the value 1 if firms have to comply to a minimum wage, year is an indicator variable taking the value 1 when in the post treatment period.
My question is how i interpret the coefficient from my 3-way interaction term, beta5. Note that the independent variable is in log, and so is the shockMW, hence it is a log-log model.
Suggestion 1: beta7 indicates the additional treatment impact, i.e. a 1% increase in the shockMW variable above the mean, the treatment effect increases by an additional beta5 percent.
Suggestion 2: treated firms with a a 1% increase in the shockMW variable above the mean experience beta5 percent treatment effect relative to the untreated firms.
I have interpreted beta2 as the treatment effect.
Thanks in advance!
I would greatly appreciate advice on interpreting a 3-way interaction between two dummy variables (treatment indicator and post-treatment-period indicator) and 1 continuous variable. Specifically, I am estimating a DiD model to evaluate the impact of a minimum wage increase. I have two periods: one pre-MW-reform-period and one post-MW-reform-period. The minimum wage is nominal and uniform across the entire country. However, inflation rates vary across states. I anticipate that the effect of the MW will be greatest, where the minimum wage has increase the most in real terms. Thus, I have made a variable, shockMW, which is captures the change in the minimum wage measured in 2018 prices, ln(real MW post/real MW pre). I have subtracted the mean value of the shock variable, so that it is evaluated at the mean.
To evaluate whether the impact of the MW increase is largest in these areas, I have estimated the following model:
Using the following code:
reghdfe lnwage treat##year##c.shockMW, absorb(FirmID) vce(cluster FirmID)
Treat is an indicator taking the value 1 if firms have to comply to a minimum wage, year is an indicator variable taking the value 1 when in the post treatment period.
My question is how i interpret the coefficient from my 3-way interaction term, beta5. Note that the independent variable is in log, and so is the shockMW, hence it is a log-log model.
Suggestion 1: beta7 indicates the additional treatment impact, i.e. a 1% increase in the shockMW variable above the mean, the treatment effect increases by an additional beta5 percent.
Suggestion 2: treated firms with a a 1% increase in the shockMW variable above the mean experience beta5 percent treatment effect relative to the untreated firms.
I have interpreted beta2 as the treatment effect.
Thanks in advance!
