Hi,
I'm correlating rater accuracy to rater experience (measured as number of examinations preformed annually). These are not normally distributed, but likely monotonically related (the more experienced, the more accurate), at least that is the hypothesis I wanna test. Thus, I wanna do Spearmans correlation.
This is my table
The sum of d^2 is 235. There are a few ties, for example rater 8, 12, 13 and 14 all claim to assess 20 cases annually, ranking third, fourth, fifth, sixth, thus having the average rank of 4.5.
Plugging it into the rho formula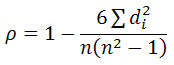
using an Excel sheet gives rho= 0.5803
With Stata:
Number of obs = 15
Spearman's rho = 0.5731
Now, I think it has to do with how Stata handle ties. In "A Gentle introduction to Stata", chapter 8, p. 180, it says that Stata uses averages when there is ties, but I have not been able to confirm this from within Stata help files. And then I don't understand why I get a discrepant result, since I averaged ranks across ties.
When instead using the rho formula for ties,
I can extend my table with xi-x(bar), yi-y(bar), and those squared
The sum of (xi-x(bar))*(yi-y(bar)) in the numerator is 8.148275586. The sum of (xi-x(bar))^2 is 0.09124059 and the sum of (yi-y(bar))^2 is 4865.6. Those two sum multiplied is 443.940198, and the squareroot of that is 21.0698884, which goes in the denominator, giving a rho of 8.148275586/21.0698884 = 0.3867261, making me even more confused.
Can this have to do with the (pre-view) findings by Hodges and collegues that standard non-parametric test in Stata, SAS, SPSS and R can give different results https://psyarxiv.com/zem2w/download ?
I know I could use Kendalls tau when there are ties, but that is besides the point.
The table with my calculations can be found at https://docs.google.com/spreadsheets...it?usp=sharing
BR,
Rasmus Green
I'm correlating rater accuracy to rater experience (measured as number of examinations preformed annually). These are not normally distributed, but likely monotonically related (the more experienced, the more accurate), at least that is the hypothesis I wanna test. Thus, I wanna do Spearmans correlation.
This is my table
| Rater | Accuracy | # of cases | Accuracy rank | Case rank | d | d2 |
| Rater 1 | 79.3% | 40 | 10.5 | 11 | -0.5 | 0.25 |
| Rater 2 | 82.8% | 40 | 13 | 11 | 2 | 4 |
| Rater 3 | 70.7% | 15 | 4 | 1.5 | 2.5 | 6.25 |
| Rater 4 | 84.5% | 23 | 14.5 | 7 | 7.5 | 56.25 |
| Rater 5 | 84.5% | 50 | 14.5 | 13 | 1.5 | 2.25 |
| Rater 6 | 75.9% | 40 | 8.5 | 11 | -2.5 | 6.25 |
| Rater 7 | 74.1% | 60 | 6.5 | 14 | -7.5 | 56.25 |
| Rater 8 | 65.5% | 20 | 3 | 4.5 | -1.5 | 2.25 |
| Rater 9 | 75.9% | 80 | 8.5 | 15 | -6.5 | 42.25 |
| Rater 10 | 79.3% | 25 | 10.5 | 8 | 2.5 | 6.25 |
| Rater 11 | 81.0% | 36 | 12 | 9 | 3 | 9 |
| Rater 12 | 72.4% | 20 | 5 | 4.5 | 0.5 | 0.25 |
| Rater 13 | 60.3% | 20 | 2 | 4.5 | -2.5 | 6.25 |
| Rater 14 | 58.6% | 20 | 1 | 4.5 | -3.5 | 12.25 |
| Rater 15 | 74.1% | 15 | 6.5 | 1.5 | 5 | 25 |
The sum of d^2 is 235. There are a few ties, for example rater 8, 12, 13 and 14 all claim to assess 20 cases annually, ranking third, fourth, fifth, sixth, thus having the average rank of 4.5.
Plugging it into the rho formula
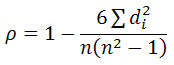
using an Excel sheet gives rho= 0.5803
With Stata:
Code:
spearman accuracy numberofcases
Spearman's rho = 0.5731
Now, I think it has to do with how Stata handle ties. In "A Gentle introduction to Stata", chapter 8, p. 180, it says that Stata uses averages when there is ties, but I have not been able to confirm this from within Stata help files. And then I don't understand why I get a discrepant result, since I averaged ranks across ties.
When instead using the rho formula for ties,

I can extend my table with xi-x(bar), yi-y(bar), and those squared
| Rater | Accuracy | Number of cases | Rank of accuracy | Rank of cases | xi-x(bar) | yi-y(bar) | (xi-x(bar))*(yi-y(bar)) | (xi-x(bar))^2 | (yi-y(bar))^2 |
| Rater 3 | 0.70689655 | 15 | 4 | 1.5 | -0.0390805 | -18.6 | 0.72689655 | 0.00152728 | 345.96 |
| Rater 15 | 0.74137931 | 15 | 6.5 | 1.5 | -0.0045977 | -18.6 | 0.08551724 | 2.1139E-05 | 345.96 |
| Rater 8 | 0.65517241 | 20 | 3 | 4.5 | -0.0908046 | -13.6 | 1.23494253 | 0.00824547 | 184.96 |
| Rater 12 | 0.72413793 | 20 | 5 | 4.5 | -0.0218391 | -13.6 | 0.29701149 | 0.00047695 | 184.96 |
| Rater 13 | 0.60344828 | 20 | 2 | 4.5 | -0.1425287 | -13.6 | 1.9383908 | 0.02031444 | 184.96 |
| Rater 14 | 0.5862069 | 20 | 1 | 4.5 | -0.1597701 | -13.6 | 2.17287356 | 0.02552649 | 184.96 |
| Rater 4 | 0.84482759 | 23 | 14.5 | 7 | 0.09885057 | -10.6 | -1.0478161 | 0.00977144 | 112.36 |
| Rater 10 | 0.79310345 | 25 | 10.5 | 8 | 0.04712644 | -8.6 | -0.4052874 | 0.0022209 | 73.96 |
| Rater 11 | 0.81034483 | 36 | 12 | 9 | 0.06436782 | 2.4 | 0.15448276 | 0.00414322 | 5.76 |
| Rater 1 | 0.79310345 | 40 | 10.5 | 11 | 0.04712644 | 6.4 | 0.3016092 | 0.0022209 | 40.96 |
| Rater 2 | 0.82758621 | 40 | 13 | 11 | 0.0816092 | 6.4 | 0.52229885 | 0.00666006 | 40.96 |
| Rater 6 | 0.75862069 | 40 | 8.5 | 11 | 0.01264368 | 6.4 | 0.08091954 | 0.00015986 | 40.96 |
| Rater 5 | 0.84482759 | 50 | 14.5 | 13 | 0.09885057 | 16.4 | 1.62114943 | 0.00977144 | 268.96 |
| Rater 7 | 0.74137931 | 60 | 6.5 | 14 | -0.0045977 | 26.4 | -0.1213793 | 2.1139E-05 | 696.96 |
| Rater 9 | 0.75862069 | 80 | 8.5 | 15 | 0.01264368 | 46.4 | 0.58666667 | 0.00015986 | 2152.96 |
The sum of (xi-x(bar))*(yi-y(bar)) in the numerator is 8.148275586. The sum of (xi-x(bar))^2 is 0.09124059 and the sum of (yi-y(bar))^2 is 4865.6. Those two sum multiplied is 443.940198, and the squareroot of that is 21.0698884, which goes in the denominator, giving a rho of 8.148275586/21.0698884 = 0.3867261, making me even more confused.
Can this have to do with the (pre-view) findings by Hodges and collegues that standard non-parametric test in Stata, SAS, SPSS and R can give different results https://psyarxiv.com/zem2w/download ?
I know I could use Kendalls tau when there are ties, but that is besides the point.
The table with my calculations can be found at https://docs.google.com/spreadsheets...it?usp=sharing
BR,
Rasmus Green

Comment